method of representing positive or negative integer
+1 if ones complement
allows for more efficient addition between negative and positive numbers
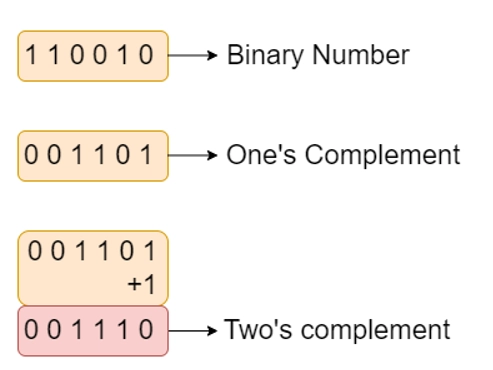
How to perform
invert the digits and add 1
Comparison
| Criteria | 1’s Complement | 2’s Complement |
|---|---|---|
| Definition | The 1’s complement of a binary number is obtained by inverting all its bits. | The 2’s complement of a binary number is obtained by adding 1 to the 1’s complement of the number. |
| Range of values that can be represented with n bits | From -2^(n-1) + 1 to 2^(n-1) – 1 | From -2^(n-1) to 2^(n-1) – 1 |
| Number of representations for zero | Can be represented in two ways (all 0s and all 1s). | Can be represented in only one way (all 0s). |
| Addition of positive and negative numbers | Same as unsigned binary addition. | Same as unsigned binary addition. |
| Subtraction of numbers | Subtract the smaller number from the larger one, then add a sign bit to the result. | Add the negative number to the positive one using binary addition. |